A computer program for solving the stagecoach problem/problems of Harvey Wagner [4]
Jsun Yui Wong
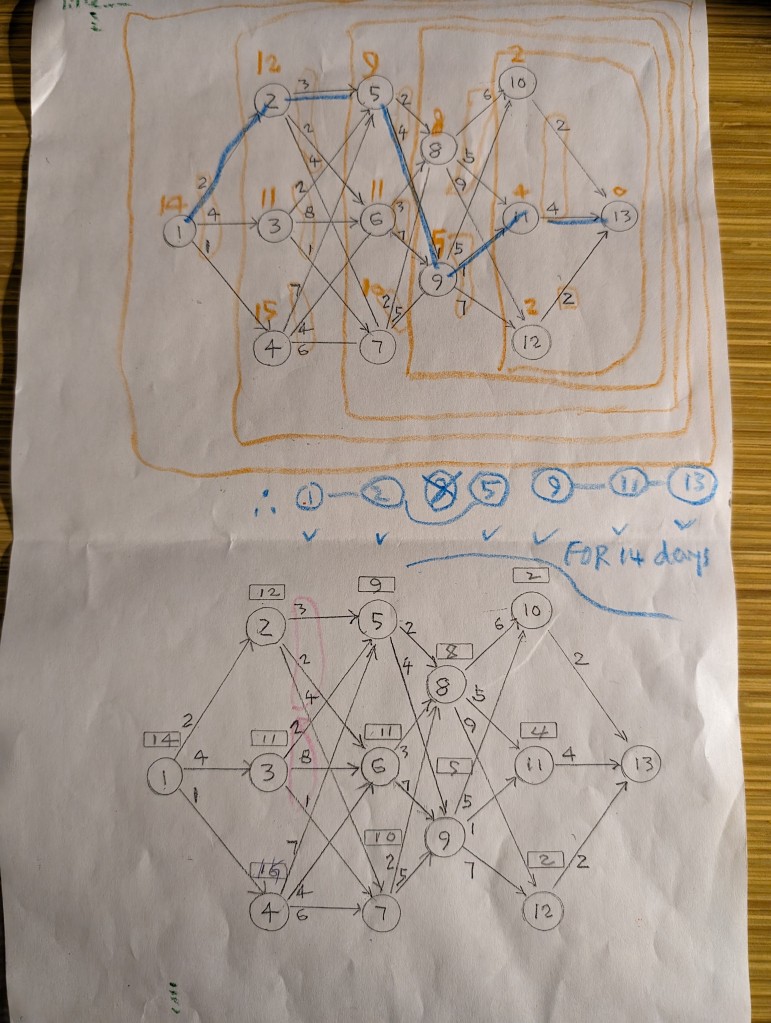
The followimg example is the stagecoach problem in Ecker and Kupferschmid [2, pp. 347-352]. Their book is available in most university libraries. It is essential that one has her/his p. 348 picture to look at; the two pictures shown below are based on their p. 348 picture, their FIGURE 10.1. This illustration is similar to Wagner’s stagecoach problem (a prototype example for dynamic programming , [3, Hillier and Lieberman, pp. 425-430]). All the good ideas in the present paper are from the five References listed below: Anderson et al. [1, pp. 820-829], Ecker and Kupferschmid [2 , pp. 347-352], Hillier and Lieberman [3, pp. 424-433], Wagner [4, pp. 262-270], and Wikipedia [5].
The computer program for the present example is as follows:

0 DEFINT J, K, B, X, A, N
2 DIM A(3513), X(3513), N(55)
81 FOR JJJJ = -32000 TO -31999
89 RANDOMIZE JJJJ
90 M = -1.5D+38
177 N(13) = 0
178 N(10) = 2 + 0
179 N(11) = 4 + 0
184 N(12) = 2 + 0
185 N(8) = 6 + 2
186 N(9) = 1 + 4
187 N(5) = 4 + 5
188 N(6) = 3 + 8
189 N(7) = 2 + 8
190 N(7) = 5 + 5
192 N(2) = 3 + 9
194 N(3) = 2 + 9
198 N(4) = 4 + 11
201 N(1) = 2 + 12
1888 PRINT N(1), N(2), N(3), N(4), N(5), N(6), N(7), N(8), N(9), N(10), N(11), N(12), N(13), JJJJ
1999 NEXT JJJJ
This BASIC computer program was run with qbv1000-win [5], and the corresponding output through JJJJ=-31999 is as follows:
14 12 11 15 9
11 10 8 5 2
4 2 0 -32000
14 12 11 15 9
11 10 8 5 2
4 2 0 -31999
The wall-clock time (NOT cpu time) for producing the output above was 2 seconds when one counts from “Starting program…”.
To find the optimal path/s, one asks: How $14 of node 1 was obtained? Through node 2 and so on. How $12 of node 2 obtained? Through node 5. How $9 of node 5 obtained? Through node 9. How $5 of node 9 obtained? Through node 11. How $4 of node 11 obtained? Through node 13. So path node 1-node 2-node 5-node-9- node 11-node 13 is an optimal path of 14 travel days. This example has only one optimal route.
References
[1] D.R. Anderson, D. J. Sweeney, I. A. Williams, An introduction to management science: quantitative approaches to decision science, ninth edition, South-Western College Publishing, 2000.
[2] J. G. Ecker, M. Kupferschmid, Introduction to operations research, John Wiley and Sons, Inc., 1988.
[3] F. S. Hillier, G. J. Lieberman, Introduction to operations research, sixth edition, McGraw Hill, Inc.
[4] Harvey Wagner, Principles of operations research, second edition, Prentice –Hall, Inc., 1975.
[5] Wikipedia, QB64, https://en.wikipedia.org/wiki/QB64.